

Den här artikeln är tänkt att ge en grundläggande förståelse för hur transmissionsledningar beter sig; när man behöver bry sig om en ledares transmissionsledningsegenskaper och vad man kan göra för att utnyttja eller tämja egenskaperna. Lämpliga bakgrundskunskaper är elementär växelströmslära, inte minst jω-metoden. Transmissionsledningar tas normalt inte upp på gymnasiet eller ens i de inledande elektrokurserna på högskolornas civilingenjörslinjer, men det betyder inte att de är särskilt svåra att begripa sig på, åtminstone inte den grundläggande teorin. Kanske kan jag med denna artikel skingra lite av den mystik som jag ibland har anat att en del personer tycker omgärdar ämnet.
Ofta tänker man sig att ledare är ideala:
Som de flesta approximationer så är approximationen att ledare är punktformiga och saknar utsträckning ypperligt bra att använda i många fall, men helt förkastlig i andra. Frågan vi ska kika på här är när induktans och kapacitans i ledare börjar spela roll och vad som händer då, dvs när man måste betrakta ledare som att de har en utsträckning i rummet. Detta kallas att kretsen är "distribuerad".
Blir allting väldigt komplicerat och obegripligt i detta fall, eller kan man fortfarande ha en intuitiv förståelse för hur saker och ting beter sig? Som tur är kommer det att visa sig att transmissionsledningar i sina enklaste former är relativt enkla att förstå och utnyttja.
Alla ledare har ett visst mått av parasitinduktans eftersom det alltid byggs upp ett magnetfält runt ledaren när ström flyter genom den. En tumregel som kan vara bra att känna till är att 1 mm ledare ofta har en induktans på ca 1 nH (i själv verket är detta en liten överskattning, 0,5 nH är kanske närmare sanningen i många fall).
Låt oss se hur stor betydelse denna induktans har i ett specifikt fall. Om vi försöker skicka en signal på 100 MHz längs 100 m kabel med induktansen 1 nH/mm, dvs totalt 100 µH så har vi alltså en serieimpedans på inte mindre än |Z| = 2×π×f×L = 2×π×100×106×100×10−6 Ω ≈ 63 kΩ. Detta verkar ju ganska mycket och borde omöjliggöra överföring av högfrekventa signaler via kabel några längre sträckor kan man tycka.
Vi tittar på ännu ett fall innan vi går vidare och listar ut var vi tänkt fel. TV-kanaler i övre UHF-bandet sänds på frekvenser över 800 MHz. Ofta används RG59-koaxialkabel när man ska överföra signalen från TV-antennen till mottagaren, t ex via ett kabel-TV-nät. En typisk impedans för en RG59-kabel är 377 nH/m. 100 m RG59-kabel borde då se ut som 2×π×800×106×377×10−9×100 ≈ 190 kΩ. I kabel-TV-nät terminerar man alltid koaxialkablarna med 75 Ω, vilket borde göra att bara 75/190 000 = 1/2500 av signalen kommer fram och det är ju en ganska kraftig dämpning.
Ännu har vi ju inte ens tagit med strökapacitansen längs ledaren i våra beräkningar. Man kan tycka att kapacitansen borde göra att signalen dämpas ännu mer. Det hela ser ju ut som ett stort LC-lågpassfilter.
Som tur är så är verkligheten inte så här besvärlig. Låt oss räkna lite noggrannare på det hela. I figuren nedan finns överst en skiss på en vanlig transmissionsledning, nämligen en så kallad mikrostripledning, dvs en ledare på ytterlagret av ett mönsterkort med ett internt jordplan under ledningen. (Det spelar egentligen ingen roll för de vidare resonemangen vilken sorts transmissionsledning det handlar om, en koaxialkabel hade gått minst lika bra.) Under skissen finns enklast möjliga elektriska modell över transmissionsledningen där vi delat upp den i korta segment med vardera längden dx. Ledningen har induktansen LL H/m och kapacitansen CL F/m. Det gör att varje segment har induktansen LL×dx och kapacitansen CL×dx. Resistansen i ledningen har vi försummat för att förenkla analysen.
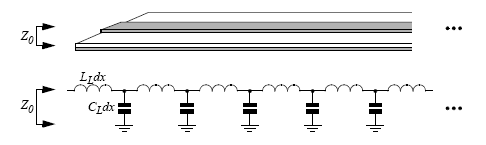
Nu ska vi försöka räkna ut vad man ser för impedans Z0 när man tittar in i början på en oändligt lång transmissionsledning enligt ovan. Att ledaren är oändligt lång betyder att modellen med spolar och kondensatorer har oändligt många segment, vart och ett med induktansen LL×dx och kapacitansen CL×dx. Att direkt ställa upp en ekvation för ett LC-nät med oändligt många komponenter verkar lite svårt, så vi får ta till ett specialtrick.
Trick: Eftersom nätet redan består av oändligt många länkar så blir impedansen densamma, nämligen Z0 om vi lägger till ännu en länk mellan mätpunkten och transmissionsledningen. Detta kan vi utnyttja för att ställa upp en ekvation för Z0:
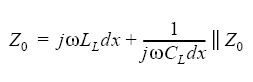
Symbolen || betecknar parallellkoppling. Om man förenklar ovanstående ekvation och sedan låter dx gå mot noll, dvs man gör indelningen i segment finare och finare, så finner man ganska enkelt följande uttryck för Z0:
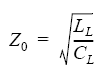
Z0 är oberoende av frekvens - bandbredden är oändlig!
Man kan därmed säga att L och C i någon mening balanserar varandra vid alla frekvenser.
Z0 är reell - den ser ut som en resistans.
Impedanser med en realdel som är större än noll absorberar energi som den inte senare kan lämna tillbaka till källan. I vanliga fall sker detta genom resistiva förluster, men vår modell består ju endast av reaktiva element och därmed är ingen värmeutveckling möjlig. Så vart tar energin vägen? Jo, energin man matar in bygger upp elektromagnetiska fält som färdas bort från källan i den oändligt långa ledningen.
I och med att Z0 är oberoende av frekvens och ledningen inte förlorar någon energi så kan alltså överföra energi utan bandbreddsbegränsning! Detta verkar ju ganska mycket bättre än våra pessimistiska kalkyler tidigare där det verkade som om induktansen och kapacitansen i ledningen gjorde att den hade en kraftig bandbreddsbegränsning.
Som sagt så färdas energi i form av elektromagnetiska fält ned längs ledningen när man skickar på en signal vid dess början. En intressant fråga är hur fort signalerna propagerar. Låt oss göra ett tankeexperiment för att reda ut detta:
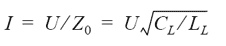
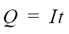
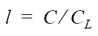
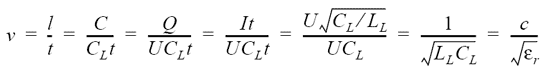
Det sista steget i formeln, att hastigheten skulle vara lika med ljushastigheten c delat med roten ur den relativa dielektricitetskonstanten εr för ledningens isolerande material (dielektrikum) tänker jag inte bevisa inom ramen för denna artikel, men sambandet kan ändå vara bra att känna till för att få lite känsla för utbredningshastigheten i ledare. Ska man vara riktigt nogräknad borde det stå en till faktor bredvid εr i formeln, nämligen μr, den relativa permittiviteten för materialet, men för alla rimliga material man kan ha som isolation i transmissionledningar är μr så gott som exakt 1, så denna faktor har plockats bort för enkelhets skull.
c är ju som bekant ungefär 3×108 m/s och εr varierar från 1 för luft upp till kanske 10 för rimliga isolationsmaterial.
Som exempel kan nämnas att det vanliga glasfiberlaminatet FR4 som ofta används i mönsterkort har ett εr på ca 4,7, vilket gör att transmissionsledningar där det elektriska fältet utbreder sig helt och hållet i laminatet har en hastighet på ca 46 % av ljushastigheten. Detta gäller så kallade striplines, dvs ledare som går inuti mönsterkort mellan två jordplan. För mikrostrip, dvs ledare som går på ett ytterlager i kortet och som har ett jordplan under sig kommer en stor del av fältet att breda ut sig i luften ovanför ledaren och signalhastigheten beror då på ett viktat medelvärde av luftens εr (1) och εr för laminatet (4,7). En sådan ledning blir alltså snabbare än en ledning på ett innerlager.
Vill man ha en ledning där signalerna färdas snabbt ska man alltså se till att använda en isolering med lågt εr, helst luft. Det finns koaxialkablar där isoleringen består mest av luft genom att man använder en sorts skumplast. Sådana kablar är alltså snabba.
Låt oss stanna upp en stund och fundera lite över vad vi kommit fram till och om slutsatserna verkligen kan stämma. Vår modell av ledningen ovan ser ut som ett lågpassfilter med en massa induktanser i serie med signalen och en massa kondensatorer ned mot jord. Hur kan en sådan koppling ha oändlig bandbredd?
Här är en lite handviftande förklaring till hur detta kan komma sig:
Hemligheten är att trots att modellen med spolarna och kondensatorerna hela tiden ser ut som ett lågpassfilter när man förfinar den genom att dela upp ledningens induktans och kapacitans i allt fler segment med allt mindre värden så får varje segment större och större bandbredd. En halvering av dx gör att bandbredden i varje segment dubbleras. Samtidigt får man ju också dubbelt så många segment och det är inte uppenbart att det skulle motverka bandbreddsökningen fullt ut. Situationen kompliceras ytterligare av att segmenten påverkar varandra och det blir inte alls särskilt tydligt vad som händer med bandbredden när man minskar dx och antalet segment ökar.
I själva verket händer en trevlig sak när man delar upp en lednings induktans och kapacitans i allt fler små LL×dx och CL×dx, nämligen att trots att den totala induktansen och kapacitansen är lika stor så sprids exciteringen av dem ut i tiden och bandbreddsbegränsningen byts mot en tidsfördröjning.
Om man tänker sig en ledning med en viss kapacitans och induktans som man exciterar med ett steg i ena änden så kommer enligt vårt resonemang steget att komma fram oförvrängd i andra änden av ledningen efter en viss tid. Innan fördröjningstiden gått händer dock inget alls i andra änden. Om man istället gör samma experiment med en diskret spole och en diskret kondensator med samma induktans och kapacitans som ledningen totalt har får man direkt en reaktion vid andra änden av ledningen, men spänningen segar sig upp i maklig takt som den brukar göra när man skickat ett steg genom ett lågpassfilter:
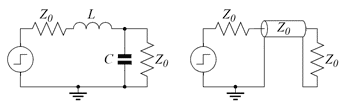
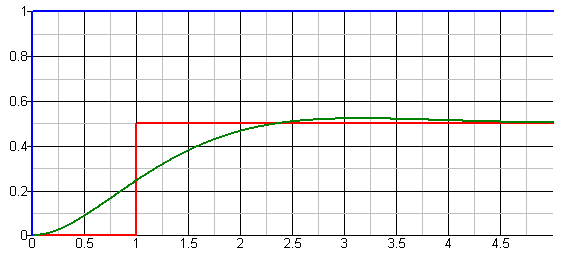
Den blå kurvan visar källans spänning medan den gröna visar vågformen efter LC-filtret och den röda visar spänningen efter transmissionsledningen.
Genom att induktansen och kapacitansen är distribuerad över ledningen så kommer bara en infinitesimal LC-länk i taget att behöva laddas upp av fronten på steget. I och med detta så tar det längre tid innan den sista LC-länken börjar exciteras än i fallet att man bara har en diskret induktans och kapacitans ovan, men denna ökade fördröjning har man alltså fått igen genom en ökad bandbredd.
Att man kan byta fördröjning mot bandbredd är i själva verket en fundamental princip hos högfrekvenskretsar och utnyttjas bl a i sk distribuerade förstärkare som är intressanta om man vill få ut maximal bandbredd ur en given sorts förstärkarelement med kapacitiv inimpedans som fälteffekttransistorer eller radiorör.
Signaler på en transmissionsledning kan färdas åt båda hållen på ledningen eftersom det inte finns något i ledningen som gör att det skulle vara någon skillnad mellan de två riktningarna. Vidare kan signalerna färdas oberoende av varandra eftersom alla element i ledningen (kapacitansen och induktansen) är linjära. Detta innebär att den totala strömmen i en punkt på ledningen är summan av strömmen för den signal som går åt höger och strömmen hos den signal som går åt vänster. På samma sätt är spänningen i en punkt lika med summan av spänningen för signalerna som går åt de båda hållen.
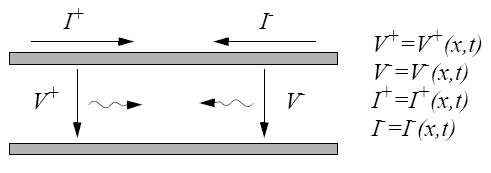
Uttrycken ovan uttrycker explicit att spännings- och strömkomponenterna hos signalerna beror både av tiden (t) och positionen (x) längs ledningen.
En signal består av en spännings- och en strömkomponent i förhållandet V+/I+ = Z0.
Spänningen i en punkt på ledningen är (superposition):
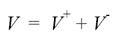
Strömmen i en punkt på ledningen är (obs minus eftersom strömmarna är definierade som positiva i olika riktningar):
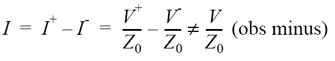
Observera att förhållandet Z0 mellan spänning och ström gäller för var och en av signalerna (den höger- respektive vänstergående) men alltså oftast inte för summan av de två motriktade signalerna.
Man talar ofta om vågor som färdas längs ledningen istället för om signaler, strömmar eller spänningar. Det här är en avgörande skillnad i hur man ser på signaler i distribuerade system jämfört med i diskreta system.
Ovan har vi behandlat oändligt långa transmissionsledningar, men det är ju aningen vanligare att man har ledningar med ändlig längd. Nu är det dags att lista ut hur ändliga ledare beter sig.
Vad händer med en våg som kommer fram till slutet av en transmissionsledning? Låt oss betrakta fallet där slutet på ledningen är kopplad till en impedans, ZL.
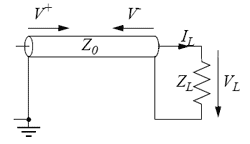
Vi har sett att det på ledningen kan finns två spänningsvågor V+ och V− som färdas åt olika håll. Dessa vågor åtföljs av strömvågorna I+ = V+/Z0 och I− = V−/Z0.
Den totala spänningen och strömmen i en punkt är V=V++V− och I=I+-I−. Notera återigen att förhållandet mellan den totala spänningen och strömmen inte nödvändigtvis har föhållandet Z0, dvs V/I≠Z0.
Vid termineringensimpedansen ZL gäller enligt Ohms lag VL=ZL×IL. Samtidigt gäller ovanstående formler för de två vågorna precis vid änden av ledningen där termineringen är inkopplad. Sätter vi ihop formlerna får vi:
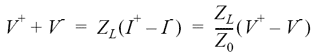
Om man löser ut V− ur ovanstående ekvation får man:
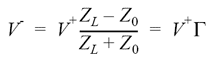
Där man har definierat reflektionskoefficienten Γ enligt:
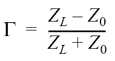
Uttrycket ovan för V− som funktion av V+, Z0 och ZL visar att om man skickar in en våg V+ mot termineringen så reflekteras en våg V− tillbaka.
När en våg kommer fram till slutet av en transmissionsledning och där träffar på en impedans ZL så reflekteras alltså en våg V− tillbaka. Ur uttrycket för reflektionskoefficienten Γ kan man göra några observationer om vad som händer i olika specialfall. Vi utgår från nedanstående generella kopplingsschema med impedans för drivare, ledning och last och studerar några specialfall:
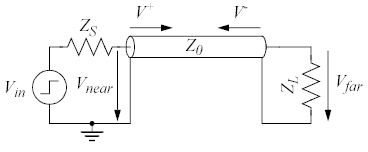
I det här fallet är källans, ledningens och lastens impedanser lika stora:
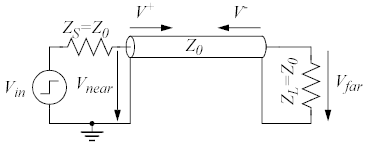
Eftersom ZL = Z0 så blir Γ = 0 och därmed får man ingen reflekterad våg, dvs V− = 0.
Tänker man efter lite är detta ganska naturligt. När man tittar in i en oändligt lång ledning ser man ju impedansen Z0 och om vi istället för lasten Z0 hade haft en oändligt lång ledning med impedansen Z0 inkopplad så hade ju vågen bara fortsatt in i ledningen utan att reflekteras. Vågen kan ju knappast "se skillnad" på om impedansen den möter kommer från en ledning eller en diskret impedans, så den reflekteras lika mycket när den ser den diskreta impedansen Z0 som om ledningen fortsatt, dvs den reflekteras inte alls.
Nedan visas de olika vågformerna i detta fall:
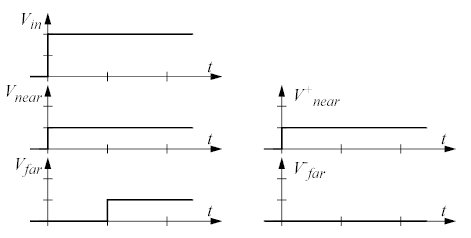
Tidsaxeln är graderad med ett streck för varje ledningsfördröjning.
Notera att vågen på ledningen har halva källans amplitud eftersom källan råkar ha impedansen Z0 och det därför uppstår en spänningsdelning mellan källimpedansen och ledningens impedans. Notera också att Vfar är en tidsfördröjd kopia av Vnear.
Det här är ett vanligt sätt att använda transmissionsledningar. Man terminerar slutet på ledningen med den karakteristiska impedansen och åstadkommer på så vis en signalöverföring utan förvrängning (men med en fördröjning).
I det här fallet är lasten en kortslutning:
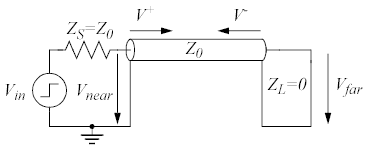
Eftersom ZL = 0 så blir Γ = -1 och därmed får man en reflekterad våg som är lika stor som den inkommande, men med motsatt polaritet, dvs V− = -V+.
Det här är inte så konstigt. Över kortslutningen kan man ju inte få någon spänning, så för att V = V+ + V− = 0 vid lasten så måste ju den reflekterade spänningen vara lika stor som − och ha ombytt tecken mot − den inkommande spänningen.
Nu har vi ju äntligen en reflekterad våg att undersöka. Låt oss se vad som händer när den färdas tillbaka till källan. När vågen kommer fram ser den impedansen Z0 eftersom den drivande spänningskällan har denna impedans. Som vi såg i förra fallet får man inte någon ytterligare reflektion om man stöter på en terminering som har samma impedans som ledningen.
Nedan visas de olika vågformerna i detta fall:
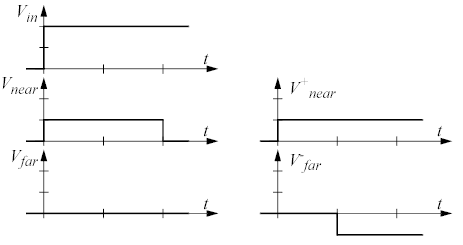
Tidsaxeln är graderad med ett streck för varje ledningsfördröjning. Allting börjar precis som i förra fallet. Vågen skickas iväg från källan ned längs ledningen och amplituden är densamma som i förra fallet. Men när vågen når fram till bortre änden får vi en negativ reflektion som gör att någon spänning aldrig syns vid den kortslutna änden (men märk väl att där flyter en ström). Den reflekterade vågen börjar röra sig till vänster i ledningen och släcker ut den totala spänningen i varje punkt den når till 0V. När den kommer fram till början så går även spänningen här ned till 0V och eftersom källimpedansen är lika med ledningsimpedansen blir det ingen ytterligare reflektion.
Vid början av ledningen fick vi alltså en puls med samma längd som två ledningsfördröjningar. Det här kan utnyttjas i speciella sammanhang när man vill åstadkomma korta pulser med väldefinierad längd. Man bygger helt enkelt en krets som skapar ett steg med en så brant flank man vill ha och låter sedan denna krets driva en kortsluten transmissionsledning av önskad längd.
Kul att veta: En av de mer extrema tillämpningarna av denna princip finns i så kallade tidsdomän-reflektometrar (TDR-instrument) som skickar in mycket branta flanker i transmissionsledningar och samplar den reflekterade signalen för att se hur steget reflekterades längs ledningen. Samplingskretsen behöver extremt korta pulser för att man ska få noggrann upplösning längs ledningen och dessa samplingspulser skapas genom att man låter en sk step-recovery-diod skapa en brant flank som man skickar in i en kort stump kortsluten transmissionsledning. Transistorkretsar är helt enkelt för långsamma för att hinna med i dessa sammanhang när man vill ha en upplösning på enstaka mm längs ledningen man mäter på.
I det här fallet är lasten en öppen krets:
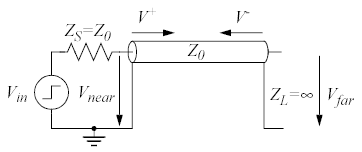
Eftersom ZL = ∞ så blir Γ = 1 och därmed får man en reflekterad våg som är lika stor som den inkommande och har samma polaritet, dvs V− = V+.
Det här är inte så konstigt. Genom den öppna kretsen kan man ju inte få någon ström att flyta, så för att I = I+ - I− = 0 vid lasten så måste ju den reflekterade strömmen vara lika stor som - och ha samma tecken som - den inkommande strömmen. (Kom ihåg att srömmarna för vågorna är definierade som positiva i vågornas färdriktning, vilket gör att de tar ut varandra om de är lika stora.)
Den reflekterade vågen färdas precis som i förra fallet tillbaka till källan och termineras där i källimpendansen utan att orsaka ytterligare reflektioner.
Nedan visas de olika vågformerna i detta fall:
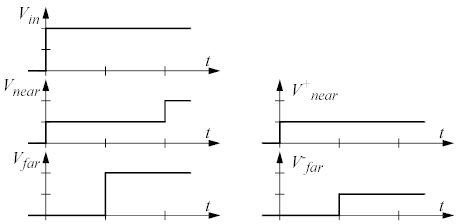
Tidsaxeln är som vanligt graderad med ett streck för varje ledningsfördröjning. Allting börjar också precis som vanligt. Vågen skickas iväg från källan ned längs ledningen och amplituden är densamma som i förra fallet, dvs halva amplituden hos källan. När vågen når fram till bortre änden får vi en positiv reflektion som gör att spänningen som dyker upp vid änden är lika stor som källans spänning, dvs dubbelt så stor som spänningen hos den högergående vågen. Den reflekterade vågen börjar röra sig till vänster i ledningen och höjer den totala spänningen i varje punkt den når till samma som källans spänning. När den kommer fram till början så går även spänningen här upp till Vin och eftersom källimpedansen är lika med ledningsimpedansen blir det ingen ytterligare reflektion.
Vid slutet av ledningen fick vi alltså en flank med samma utseende som den flank som källan skickade in före källimpedansen. Det här är ett fenomen som man ofta utnyttjar vid punkt-till-punktförbindelser. Man serieterminerar källan med samma impedans som ledningen har och ser till att mottagaränden har en hög (om än inte oändlig) impedas vid de frekvenser man är intresserad av (typiskt är mottgaren en CMOS-ingång) så att man får (nästan) hundraprocentig reflektion vid mottagaren och därmed samma utseende och amplitud på vågformen där som man har före källimpedansen.
När allting stabiliserat sig dras inte längre någon ström från källan och detta är därmed en ganska strömsnål metod att terminera ledningar, speciellt om signalkällan inte ändrar sig så ofta relativt hur lång ledningsfördröjningen är.
I det här fallet har källan en betydligt lägre impedans än ledningen och lasten har mycket högre impedans än ledningen. Fallet illustrerar vad som händer om man har flanker som är snabba relativt ledningsfördröjningen och inte har brytt sig om att terminera.
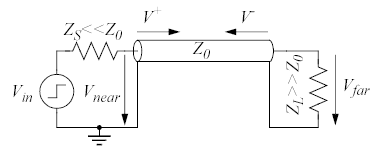
Eftersom ZL ≈ ∞ så blir Γ ≈ 1 vid lasten och därmed får man en reflekterad våg som är nästan lika stor som den inkommande och har samma polaritet, dvs V− ≈ V+. Vidare blir Γ ≈ -1 vid källan och därmed får man stora negativa reflektioner i denna ände av ledningen när det kommer in vågor mot den. Vi har alltså en situation där vågor kommer att reflekteras mot båda ändarna av ledningen och istället för att allt lugnar ner sig efter en eller två ledningsfördröjningar får vi nu ett skådespel som håller på längre innan det klingar av. Om källimpedansen är riktigt låg och lastimpedansen riktigt hög så dröjer det lång tid innan reflektionerna dör ut. Vågformerna nedan visar hur det kan se ut (ZS=5Ω, Z0=50Ω, ZL=1kΩ):
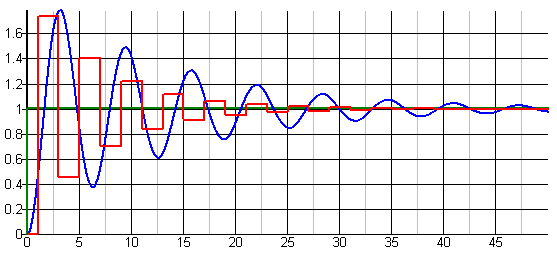
Ledningsfördröjningen är 1 tidsenhet och den röda vågformen visar spänningen vid lasten medan den gröna visar vid spänningskällan. Man ser hur spänningen på lasten "ringer" pga den dåliga termineringen, ungefär som vid en svagt dämpad LC-krets. Den blå kurvan har lagts in som jämförelse och är spänningen över lasten i en krets där transmissionsledningen har ersatts med en enda LC-länk med samma totala induktans och kapacitans som hos ledningen. Även om både perioden och amplituden avviker något mellan de två fallen så ser man släktskapen i beteende mellan kretsarna.
Ringning är så gott som alltid ett oönskat fenomen och man drabbas av det när man har en ledning vars fördröjning är för lång relativt flanktiden och man inte har terminerat ledningen. En tumregel är att man drabbas av ringningar om ledningsfördröjningen är längre än en sjättedel av stigtiden hos signalen.
Observera att det inte spelar någon som helst roll hur låg frekvensen på signalen är för om man drabbas av ringning eller inte, utan det viktiga är flanktiden. Även om man har en så låg klockfrekvens som 1 Hz, men med en stigtid på t ex bara 3 ns så drabbas man av kraftig ringning redan vid en ledning som bara är någon decimeter lång. En snabb mottagare av klocksignalen hinner antagligen reagera på ringningen och klockas därmed flera gånger vid varje klockflank, vilket antagligen får hela systemet att inte fungera.
I detta exempel med en låg klockfrekvens är det smartast att motverka ringningen genom att göra flanken långsammare (det hjälper även mot problem med utstrålade störningar, EMI), men i andra fall när man måste ha snabba flanker är rätt lösning att terminera ledningen på ett lämpligt sätt för att förhindra oönskade reflektioner.
Ett användningsområde för en helt "felterminerad" stump transmissionsledning som i fallet ovan är i bandpass- och bandspärrfilter i radiosammanhang där man kan utnyttja de väldigt höga Q-värden som man ganska enkelt får med transmissionsledningar. Det är ofta betydligt svårare att åstadkomma lika branta filter vid höga frekvenser med hjälp av diskreta komponenter.
I det här fallet har både källan och lasten hög impedans jämfört med ledningen. Fallet illustrerar vad som händer när man har en elektriskt lång transmissionsledning (dvs en ledning där fördröjningen är åtminstone i samma storleksordning som flanktiderna hos signalerna) i en omgivning av kretsar med högre impedans, t ex om man har en svag drivare och en oterminerad ledning.
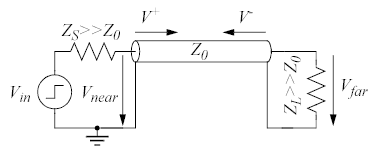
Eftersom ZL >> Z0 så blir Γ ≈ 1 vid lasten och därmed får man en reflekterad våg som är nästan lika stor som den inkommande och har samma polaritet, dvs V− ≈ V+. Vidare blir Γ ≈ 1 även vid källan och därmed får man reflektioner även i denna ände av ledningen när det kommer in vågor mot den. Källan har en hög impedans jämfört med ledningen och därför blir den initiala amplituden på ledningen låg.
Ett litet initialt steg reflekteras alltså mot lasten och ökar på den totala spänningen på ledningen. Vågen reflekteras sedan mot källan igen och ökar amplituden ytterligare. Så här fortsätter det med gradvis minskad amplitud hos de reflekterade vågorna (och gradvis ökande amplitud på den totala spänningen) tills man uppnår ett asymptotiskt värde på spänningen som bestäms av spänningsdelning mellan källan och lasten. Så här kan vågformerna se ut (ZS=1kΩ, Z0=50Ω, ZL=10kΩ):
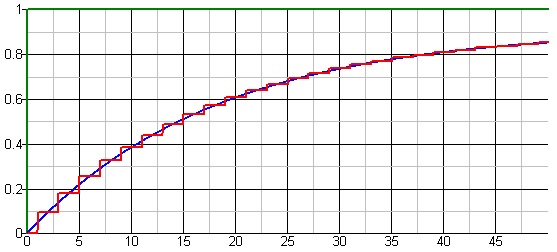
Ledningsfördröjningen är 1 tidsenhet och den röda vågformen visar spänningen vid lasten. Man ser hur spänningen stiger med exponentiellt avtagande hastighet, ungefär som när man laddar en kondensator genom ett motstånd. Den blå kurvan visar vågformen där man ersatt ledningen med en kapacitans till jord med samma värde som ledningens totala kapacitans. Kurvorna följer varandra perfekt, vilket antyder att det är ledningens kapacitans som i första hand bestämmer hur kretsen beter sig i detta fall när impedanserna kring ledningen är betydligt högre än Z0.
Det finns väldigt mycket skrivet om transmissionsledningar och signalintegritet. Här är några av de böcker jag tycker är att rekommendera:
High-Speed Digital Design: A Handbook of Black Magic
High Speed Signal Propagation: Advanced Black Magic
The Design of CMOS Radio-Frequency Integrated Circuits, Second Edition